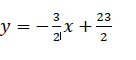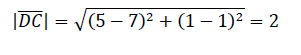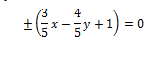contoh soal garis sebagai kurva berderajat satu

Contoh 1

Sebuah garis yang melalui titik A(1, 2), B(-3, 4), dan C(5, 0) maka persamaan kurva berderajat satu untuk garis tersebut ditentukan sebagai berikut;

Langkah 1.

Subtitusikan titik A, B, dan C ke dalam persamaan kurva

Garis melalui A(1, 2) => A(1) + B(2) + C = 0

                              =>         A + 2B + C = 0                       (pers 1)

Garis melalui B(-3, 4)=>A(3) + B(-4) + C = 0

                    =>     -3A + 4B + C = 0                       (pers 2)

Garis melalui C(5, 0) =>A(5) + B(0) + C = 0

                               =>               5A + C = 0

                               =>                         C=-5A                      (pers 3)

Langkah 2.

Subtitusikan (3) ke (1)

      A + 2B + C = 0

A + 2B + (-5A) = 0

           2B – 4A = 0

                   2B = 4A

                      B = 2A                          (pers 4)

Langkah 3.

Subtitusikan (3) dan (4) ke persamaan kurva

Ax + By + C = 0

Ax + 2Ay – 5A = 0

Misalkan: A = 1

x + 2y – 5 = 0

 

Contoh  2

Persamaan kurva berderajat satu pada contoh 1 dapat diubah menjadi persamaan garis bergradien dengan langkah sebagai berikut.

x + 2y - 5 = 0 => 2y = -x + 5

          => 𝒚= −𝟏𝟐𝒙+ 𝟓𝟐

maka gradien garis yang melalui titik A(1, 2), B(-3, 4), dan C(5, 0) adalah m = - ½ yaitu bergradien negatif. Sudut inklinasi yang dibentuk garis tersebut yaitu :

Contoh 3:
Deskripsikan bentuk masing-masing garis berdasarkan gradien dan sudut inklinasi yang ditunjukkan pada gambar berikut.

Penyelesaian :

Diketahui : Empat garis berbeda p = AB, q = AC, r = BC, dan s = BD

Ditanyakan : Bentuk garis p, q, r dan s berdasarkan gradien dan sudut inklinasi … ?

Identifikasi masalah : Tiap garis melalui paling sedikit dua titik berbeda. Jika diketahui koordinat kedua titik yang dilalui garis maka dapat ditentukan persamaan garis bergradien dengan menggunakan metode penyelesaian sistem persamaan linier dua variabel. Atau dapat menggunakan konsep trigonometri pada segitiga siku-siku untuk menentukan gradien suatu garis. Sebagai contoh garis p = AB melalui titik A(1, 1) dan B(5, 4). Ruas garis AB merupakan hipotenusa dari segitiga siku-siku ADB. Kemiringan garis AB membentuk sudut BAD sehingga kemiringan garis dapat ditentukan dari nilai tangen ukuran sudut BAD

Sudut inklinasi garis ditentukan dengan mencari nilai arc tan dari gradien.

Langkah penyelesaian :

Cara 1 : Metode penyelesaian sistem persamaan linier dua variabel (SPLDV) untuk garis r=BC yang melalui titik B(5, 4) dan C(7, 1)

Langkah 1 : Substitusi koordinat titik-titik ke dalam persamaan garis y = mx + c

Garis melalui titik B(5,4) => 4 = 5m + c

Garis melalui titik C(7,1) => 1 = 7m + c

Langkah 2 : Metode eliminasi SPLDV

Langkah 3 : Substitusi nilai m dan c ke dalam persamaan garis y = mx + c

Persamaan garis yaitu 

Cara 2 : Metode pencarian nilai tangen

 

Langkah 1 : Membuat segitiga siku-siku dengan hipotenusa adalah ruas garis dari dua titik pada garis

Segitiga siku-siku yang dapat dibuat dengan hipotenusa ruas garis BC yaitu segitiga BDC.

Langkah 2 : Menentukan panjang sisi alas dan sisi tegak segitiga

Sisi alas segitiga BDC adalah ruas garis DC dan sisi tegak segitiga BDC adalah ruas garis BD. Panjang masing-masing ruas garis dicari dengan menggunakan rumus jarak antara dua titik.

 

Langkah 3 : Menentukan nilai tangen sudut yang dibentuk oleh hipotenusa segitiga siku-siku Sudut yang dibentuk antara hipotenusa ruas garis BC dan sisi alas ruas garis DC yaitu segitiga DCB. Berdasarkan gambar di atas dapat dilihat bahwa segitiga DCB berada di kuadran II yaitu pada interval

Oleh karena itu nilai tangent sudut pada kuadran tersebut adalah negatif. Maka nilai dari tangent sudut tersebut dicari sebagai berikut.

Langkah 4 : Menentukan besar sudut inklinasi

Sudut inklinasi garis r = BC yaitu :

Langkah 5 : Deskripsi bentuk garis berdasarkan gradient dan sudut inklinasi

Garis r memiliki gradien 𝑚= −3/2 yaitu bergradien negatif yang ditunjukkan dengan bentuk garis dari kiri atas ke kanan bawah dengan besar sudut inklinasi membentuk sudut tumpul sekitar 123,69 derajat.

Contoh 4:

Gambarkan dan tentukan persamaan garis-garis yang masing-masing memiliki gradien m = 1 dan melalui salah satu titik berikut. Garis h melalui titik O(0,0), garis k melalui titik K(2, 3) dan garis l melalui titik L(-2, -3)

Penyelesaian :

Diketahui : Tiga garis h, k dan l masing-masing bergradien mh = mk = ml = 1.

Tiga titik O(0, 0), K(2, 3), dan L(-2, -3) masing-masing dilalui garis h, k, atau l.

Ditanyakan : Gambar dan persamaan garis h, k dan l … ?

Identifikasi masalah : Jika diketahui gradien garis dan sebuah titik yang dilalui garis tersebut maka persamaan garis dapat ditentukan dengan cara mensubtitusikan nilai gradien dan koordinat titik ke dalam persamaan garis bergradien m yaitu y = mx + c. Misalkan garis memiliki gradien m dan melalui titik (x0, y0) maka diperoleh persamaan : y0 = m.x0 + c

selanjutnya dapat diselesaikan dengan tahapan berikut

 

Persamaan yang diperoleh dinamakan persamaan garis bergradien m dan melalui sebuah titik (x0, y0). Untuk dapat menggambarkan garis maka perlu ditentukan sudut inklinasi garis tersebut dengan menggunakan rumus

Langkah penyelesaian :

Langkah 1 : Substitusi koordinat titik dan gradien ke persamaan garis y - y0 = m(x - x0)

Persamaan garis h dengan mh = 1 dan melalui O(0, 0) yaitu y - 0 = 1(x - 0) => y = x

Persamaan garis k dengan mk = 1 dan melalui K(2, 3) yaitu y - 3 = 1(x - 2) => y = x +1
Persamaan garis l dengan ml = 1 dan melalui L(-2, -3) yaitu y + 3 = 1(x + 2)=> y = x - 1

Langkah 2 : Menentukan sudut inklinasi garis

Karena gradien ketiga garis sama yaitu mh = mk = ml = 1 maka sudut inklinasi garis h, k dan l yaitu 𝛼ℎ=𝛼𝑘=𝛼𝑙=𝑎𝑟𝑐tan1≈ 0,7854 𝑟𝑎𝑑=45°

Langkah 3 : Menggambar garis berdasarkan gradien dan sebuah titik

1) Buatlah titik-titik yang dilalui garis pada sistem koordinat Cartesius.

2) Buatlah sinar-sinar yang sejajar sumbu x dari masing-masing titik

3) Buatlah sinar kedua dari masing-masing titik sehingga membentuk sudut 45 terhadap sinar pertama lalu perpanjang sinar kedua sehingga membentuk garis.

Gambar garis di bawah ini menunjukkan bahwa garis k dapat diperoleh dengan menggeser garis h sejauh satu satuan ke kanan sedangkan garis l diperoleh dengan menggeser garis h sejauh satu satuan ke kiri. Jadi, konstanta c pada persamaan garis y = mx + c menjadi konstanta translasi (pergeseran) garis y = mx. Gambar tersebut juga menunjukkan bahwa ketiga garis h, k dan l yang memiliki gradien mh = mk = ml merupakan garis-garis yang saling sejajar satu sama lain.

Contoh 5:

Tentukan persamaan garis jika diketahui titik potong garis dengan sumbu koordinat Cartesius yaitu (a, 0) dan (0, b).

Diketahui : Sebuah garis yang memotong sumbu x di (a, 0) dan sumbu y di (0, b)

Ditanyakan : Persamaan garis … ?

Identifikasi masalah : Misalkan persamaan garis y = mx + c melalui (a, 0) dan (0, b). Maka substitusi koordinat titik ke dalam persamaan menghasilkan : am + c = 0 dan b = c sehingga diperoleh am + b = 0 dan gradient garis 𝑚= −b/a. Jadi persamaan garis yang melalui titik (a, 0) dan (0, b) yaitu :

Jika dua buah garis berpotongan maka akan terbentuk empat buah sudut yang berpangkal di titik sudut yang sama yaitu titik potong kedua garis tersebut seperti terlihat pada gambar di samping.

Sudut θ dibentuk oleh sinar garis 𝑅𝐵dan 𝑅𝐷 sedangkan sudut ϕ dibentuk oleh sinar garis 𝑅𝐷 dan 𝑅𝐴 .

Contoh 6:

Ubahlah persamaan garis g berikut ini menjadi persamaan normal. Kemudian tentukan jarak titik P ke garis g

g: 3x-4y+5=0 dan P(-1,3)

Penyelesaian:

 










Maka persamaan garis normalnya adalah 

Jarak dari titik P ke garis g

Maka jaraknya adalah 2cm