Vektor Pada Bidang

Vektor adalah himpunan ruas garis berarah yang mempunyai besar dan arah yang sama

Suatu vektor dapat diberi simbol dengan salah satu anggotanya sebagai wakil. misanya pada gambar diatas, ruas-ruas garis itu mempunyai besaran dan arah yang sama, maka vektor itu dapat dinyatakan dengan simbol a atau AB, CD, EF atau GH (dengan tanda panah dibawah atau diatas).

Dalam literatur ada beberapa simbol untuk wakil vektor antara lain:
1. dengan satu huruf kecil a, b, c,... yang dicetak tebal
2. dengan dua huruf besar. misalnya AB (dengan tanda panah dibawah atau diatasnya itu dimaksudkan vektor dengan titik pangkal A dan titik ujung B). Vektor seperti ini dinamakan vektor bebas.

Suatu vektor yang titik pangkal tertentu dan vektor-vektor lainnya harus mempunyai tiitk pangkal tertentu itu, maka vektor demikian disebut vektor posisi (vektor letak).

Pada gambar diatas, vektor-vektor posisi titik B, C dan D masing-masing terhadap titik A berturut-turut adalah AB, AC dan AD (dengan tanda panah diatasnya) atau u, v, w (dengan garis bawah).

1.  Penjumlahan Vektor

a. cara jajar genjang

cara ini dengan menggambarkan vektor b sehingga titik pangkalnya berimpit dengan titik pangkal  vektor a. selanjutnya dibuat garis dari ujung a sejajar b dan garis dari ujung b sejajar a, sehingga didapat bangun jajaran genjang. Maka a + b adalah vektor yang bertitik  pangkal berimpit dengan titik pangkal a dan berimpit diagonal jajaran genjang

 

b. cara segitiga

untuk memperoleh jumlah dua vektor u dan v, yaitu u + v, gambarlah vektor v yang titik pangkalnya berimpit dengan titik ujung vektor u. Maka u + v adalah vektor yang menghubungkan titik pangkal u dan titik ujung vektor v .

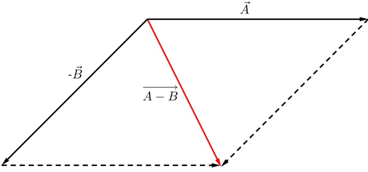
2. Pengurangan Vektor
a. cara segitiga
Lawan dari vektor B adalah vektor –B, yang mempunyai besar yang sama dengan B tetapi berlawanan arah. Maka pengurangan vektor adalah dengan menjumlahkan dengan lawan vektor kedua, yaitu  
A – B = A + (-B)
 

b. cara jajar genjang

Sama halnya dengan cara penjumlahan, tetapi vektor B mempunyai arah yang berlawanan.

Untuk sebarang vektor u, v dan w dan sebarang skalar a dan b berlaku sifat-sifat berikut ini:
1. u + v = v + u
2. ( u + v ) + w = u + ( v + w )
3. u + 0 = 0 + u = u
4. u + (- u ) = 0
5. a ( b u ) = ( a b ) u =  u ( a b )
6. a ( u + v ) = a u + a v
7. ( a + b ) u = a u + b u 


3. Perkalian Vektor

Jika u, v dan w vektor-vektor sebarang dan c suatu maka berlaku sifat-sifat berikut ini:
1. u . v = v . u
2. u  ( v  + w ) = u . v  +  u . w
3. c ( u . v ) = ( c . u  ) . v = u . ( c. v )
4. 0 . u = 0
5. u . v = 0 bila dan hanya bila u tegak lurus v atau u = 0 atau  v  =  0