Geometri Analitik: kedudukan titik dan jarak antara dua titik

TITIK DAN KURVA PADA SISTEM KOORDINAT
Hay teman-teman, selamat datang diblog saya. Perkenalkan nama saya Keke Berlinda, saya adalah mahasiswa Pendidikan Matematika di Universitas Bengkulu. Dikunjungan kalian kali ini, saya akan membahas materi mengenai titik dan kurva pada sistem koordinat. Nah materi tersebut terdapat didalam mata kuliah Geometri analitik. apakah kalian tau apa pengertian Geometri analitik tersebut? kepo kan? Mau tau kan? Yaa udah deh, sebelum kita masuk kemateri tersebut , ada baiknya kita mengetahui apa itu pengertian geometri analitik.

Geometri analitik merupakan kajian terhadap obyek-obyek geometri dengan menggunakan sistem koordinat yang diulas menggunakan konsep dan prinsip aljabar dan analisis. Perkembangan geometri analitik dimulai dengan kehadiran bentuk baru persamaan (equation) Bentuk baru persamaan tersebut memungkinkan untuk mengklasifikasikan kurva berdasarkan derajat (degree). Kurva berderajat satu adalah garis lurus (straight lines), kurva berderajat dua merupakan irisan kerucut (conic sections), dan kurva berderajat tiga dinamakan kurva kubik (cubic curves).

Nah sekarang kalian sudah tau kan apa itu geometri analitik, geomerti analitik selalu menggunakan sistem koordinat untuk mengkaji obyek-obyek geometri menggunakan konsep dan prinsip aljabar dan analisis.. kalian tau siapa yang menemukan sistem koordinat tersebut? nah yang menemukannya adalah Descartes. Descartes (sekitar tahun 1637) menggunakan bentuk persamaan baru untuk mengubah masalah-masalah geometri menjadi masalah aljabar menggunakan koordinat sehingga dapat diselesaikan dengan manipulasi aljabar.

Gambar 1. bentuk sumbu koordinat untuk menganalisis sebuah kurva secara aljabar

Dalam bukunya, Descartes (Smith & Latham, 1957) menuliskan “I choose a straight line, as AB, to attach to refer all its points…and in AB I choose a point A at which to begin the investigation… Then I draw through C the line CB parallel to GA. Since CB and BA are unknown and indeterminate quantities, I shall call one of them y and the other x.” Pernyataan Descartes tersebut mendeksripsikan mengenai sumbu koordinat x dan y. Selanjutnya Descartes menggunakan persamaan aljabar untuk mengidentifikasi kurva tersebut. Terlihat pada gambar 1, kurva EC yang dinyatakan oleh persamaan tersebut memiliki bentuk hiperbola. Diagram tersebut menjadi awal penggunaan sistem koordinat Cartesius. Penamaan sistem koordinat ini dilakukan untuk menghormati karya pemikiran Rene Descartes.

Kita sudah mengetahui apa itu geometri analitik, apa hubungan geometri analitik dengan sisitem koordinat, bagaimana bentuk sistem koordinat tersebut bahkan penemu nya kita juga sudah mengetahuinya.. nah sekarang kita akan mulai masuk kemateri titik dan kurva.. selamat membaca teman-teman

1. Kedudukan Titik-titik dan Jarak antara Dua Titik

Sebelum mengetahui apa itu kedudukan titik,kita harus tau apa yang dimaksud dengan titik.

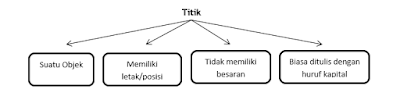
Dari ciri-ciri diatas dapat kita simpulkan bahwa titik adalah bagian terkecil dari suatu objek yang memiliki letak atau posisi, tidak memiliki besaran seperti panjang, tinggi, lebar dan lain-lain kemudian biasa ditulis dengan huruf kapital, misalnya A, B ataupun C.

Contoh gambar titik P yang terletak diantara garis g dan h.

Titik-titik pada sebuah bidang yang membentuk himpunan titik dan memenuhi suatu kriteria tertentu dinamakan kedudukan titik (locus of points). Kedudukan titik dapat dinyatakan sebagai suatu fungsi. Misalnya titik-titik pada lingkaran berjari-jari 1 cm dapat dinyatakan sebagai x² + y² = 1. Secara geometris, hanya titik-titik berjarak 1 cm dari titik pusat lingkaran tersebut yang memenuhi kedudukan titik yang dinyatakan oleh persamaan x² + y² = 1.

Teorema-teorema dasar tentang kedudukan titik-titik (Fundamental Locus Theorems) sebagai berikut.

Teorema	Gambar
Teorema 1.1 Jika ada titik P dan ada beberapa titik yang memiliki jarak yang sama dengan titik P tersebut sehingga membentuk lingkaran yang berpusat di titik P dengan ukuran panjang jari-jari d
Teorema 1.2 Jika ada 1 garis dan ada beberapa titik lain yang memiliki jarak yang sama yaitu d terhadap garis l.
Teorema 1.3 Jika ada 2 titik dan ada beberapa titik yang berjarak sama antara titik P dan Q yang membentuk garis tegak lurus dan membagi 2 sama panjang
Teorema 1.4 Jika ada titik-titik yang berjarak sama dari 2 garis sejajar yaitu l₁ dan l₂ sehingga membentuk garis yang sejajar dengan 2 garis tersebut dan terletak diantara dua garis tersebut
Teorema 1.5 Ada titik-titik yang berjarak sama dari 2 garis berpotongan yang membentuk sepasang garis berpotongan tegak lurus yang membagi 2 sama besar sudut-sudut yang dibentuk
Teorema 1.6 Ada titik-titik yang berjarak sama dari kedua sisi sebuah sudut yang membentuk sebuah garis yang membagi 2 sudut sama besar (Bisector Of Angle)
Teorema 1.7 Ada titik-titik yang berjarak sama dari dua buah lingkaran konsentris (concentric circles) yang membentuk sebuah lingkaran yang terletak diantara 2 buah lingkaran tersebut dan membentuk lingkaran yang konsentris juga.
Teorema 1.8 Ada titik-titik pada jarak tertentu dari sebuah lingkaran yang memiliki jari-jari lebih panjang dari jarak tersebut sehingga membentuk sepasang lingkaran yang konsentris
Teorema 1.9 Ada titik-titik yang berjarak tertentu dari suatu lingkaran yang berjari-jari kurang dari jarak tersebut

Kita sudah membahas tentang titik, kedudukan titik beserta teorema-teoremanya, nah sekarang kita akan membahas mengenai jarak antara dua titik.. jika ada dua titik berbeda dan terletak pada posisi yang berbeda juga, bagaimana cara menentukan jarak antara kedua titik tersebut? apakah kita bisa menebaknya dengan cara melihat langsung menggunakan kasat mata saja? Apa kita bisa menggunakan sebuah alat untuk mengukurnya? Atau mungkin kita bisa mengetahui jarak tersebut menggunakan rumus yang sudah ada? nah kalian pasti bingung kan? yukk kepoin dan baca langkah-langkah untuk menentukan jarak antara dua titik tersebut:

1) Buatlah dua titik berbeda yaitu A dan B lalu hubungkan dengan sebuah ruas garis.

2) Buat sebuah garis melalui A dan sebuah garis lain yang melalui B sehingga kedua garis berpotongan tegak lurus.

3) Tentukan titik potong kedua garis yaitu C sehingga diperoleh segitiga siku-siku ACB atau BCA lalu ukur panjang ruas garis CA dan CB

4) Tentukan panjang ruas garis AB dengan menggunakan Teorema Phytagoras :